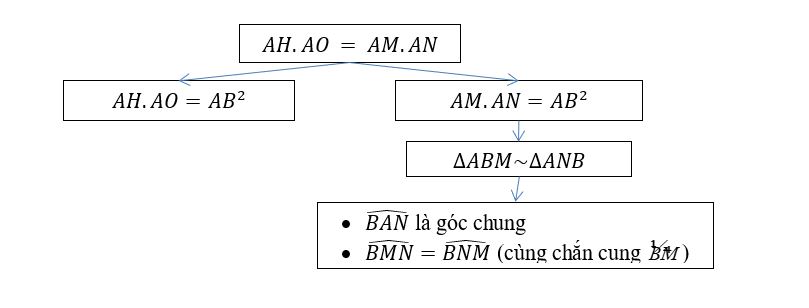
Bài toán: Từ điểm A nằm ngoài đường tròn (O;R) vẽ hai tiếp tuyến AB, AC (C, B là tiếp điểm) của (O; R), OA cắt BC tại H. Kẻ cát tuyến AMN (M nằm giữa A và N, MN không đi qua điểm O). Chứng minh: AH.AO = AM.AN.
Phương pháp:
Các bước thực hiện của phương pháp giải:
-Bước 1: Tìm hiểu nội dung của bài toán.
+ Giả thiết bài toán là gì ? Kết luận bài toán là gì ? Hình vẽ minh họa như thế nào ?
+ Những kiến thức cơ bản gắn liền với giả thiết và kết luận của bài toán là gì ?
-Bước 2: Xây dựng sơ đồ giải toán: Cần chỉ rõ các bước theo sơ đồ phân tích A ⇒B⇒C⇒⋯⇒Y⇒X.
-Bước 3: Trình bày bài giải theo các bước đã chỉ ra.
-Bước 4: Kiểm tra và nghiên cứu bài giải.
+ Xem xét các sai lầm, các trường hợp có thể xảy ra.
+ Nghiên cứu bài toán mở rộng, tương tự, lật ngược vấn đề, … (nếu có).
Cách giải: Hình thành sơ đồ tư duy:
Ngô Tùng Nho
Giáo viên Toán - Trường Quốc tế Á Châu